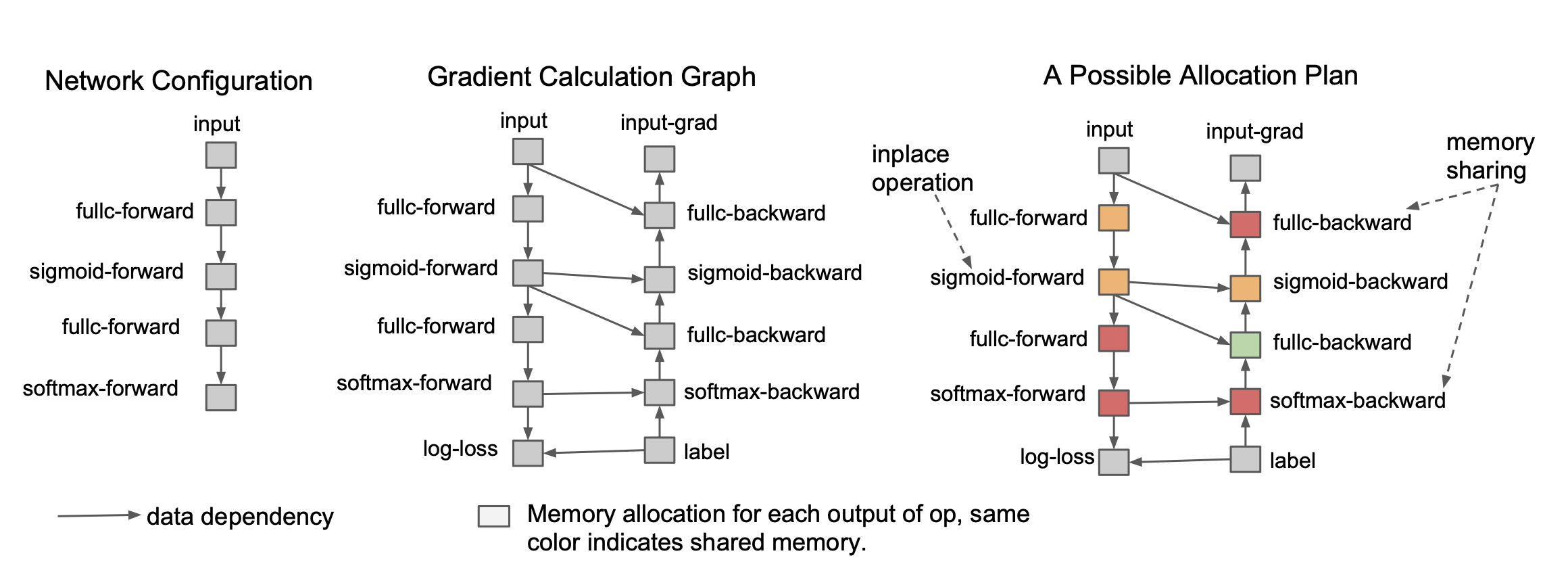
Image from the paper Training Deep Nets with Sublinear Memory Cost

An Introduction to Gradient Checkpointing

Gradient checkpointing is a powerful technique used in deep learning to address memory limitations during the backward pass of neural network training. In this blog post, we will explore the concept of gradient checkpointing and its practical implications.

Understanding Gradient Checkpointing

During the training of deep learning models, memory consumption can become a significant bottleneck, especially when dealing with large models or limited hardware resources. Gradient checkpointing offers a solution by reducing memory requirements at the cost of additional computation.

In the standard backpropagation algorithm, all intermediate activations are stored in memory during the forward pass, as they are needed to compute gradients during backpropagation. However, this can be memory-intensive, particularly for deep architectures or resource-constrained environments.

Gradient checkpointing alleviates this memory burden by selectively storing only a subset of intermediate activations, freeing up memory for other purposes. The discarded activations are then recomputed on-the-fly during the backward pass, using the stored activations as starting points.

Mathematical Example

To better grasp the concept, let’s consider a simple mathematical example. Suppose we have a deep learning model with three layers: Layer 1, Layer 2, and Layer 3. During the forward pass, the input to Layer 1 is denoted as X, and the output of Layer 3 is denoted as Y. The intermediate activations between the layers are denoted as A1, A2, and A3, respectively.

Forward Pass:

\[\begin{align*} A_1 &= \text{{Layer1}}(X) \\ A_2 &= \text{{Layer2}}(A_1) \\ Y &= \text{{Layer3}}(A_2) \end{align*}\]

During the backward pass, we need to compute the gradients of the model parameters. In standard backpropagation, all intermediate activations are used to compute these gradients. However, with gradient checkpointing, we selectively store a subset of activations and recompute the rest when needed.

Gradient Computation:

\[\begin{align*} \frac{{dY}}{{dA_2}} &= \text{{Gradient of the loss function with respect to }} Y \\ \frac{{dA_2}}{{dA_1}} &= \text{{Gradient of Layer3 with respect to }} A_2 \\ \frac{{dA_1}}{{dX}} &= \text{{Gradient of Layer1 with respect to }} X \end{align*}\]

For instance, let’s assume we decide to checkpoint the activation A1. During the backward pass, we recompute A1 using Layer1(X), and then proceed with the gradient computation for the remaining layers.

Recomputation of A1:

\[A_1 = \text{{Layer1}}(X)\]

Continued Gradient Computation:

\[\begin{align*} \frac{{dA_2}}{{dA_1}} &= \text{{Gradient of Layer2 with respect to }} A_1 \\ \frac{{dY}}{{dA_2}} &= \text{{Gradient of the loss function with respect to }} Y \end{align*}\]

By recomputing the discarded activations, we reduce memory usage while sacrificing additional computation time. This trade-off allows us to train larger models or increase batch sizes, leading to improved performance or better utilization of available resources. Benefits and Trade-offs

Gradient checkpointing offers several benefits in the context of deep learning:

Memory Reduction:

By selectively storing and recomputing intermediate activations, gradient checkpointing reduces memory requirements during the backward pass, making it possible to work with larger models or limited resources.

Flexibility:

Gradient checkpointing is a flexible technique that can be applied to various network architectures and frameworks without requiring significant modifications to the model structure or training pipeline.

However, it’s essential to consider the trade-offs associated with gradient checkpointing:

Computational Overhead:

Recomputing intermediate activations during the backward pass introduces additional computational overhead, which can extend the overall training time. The extent of this overhead depends on the complexity of the model and the number of recomputations required.

Algorithmic Complexity:

Implementing gradient checkpointing requires careful consideration of the computational graph and identifying the appropriate checkpoints. This process can be complex, especially for large and intricate network architectures.

Conclusion

Gradient checkpointing is a valuable technique for mitigating memory limitations in deep learning. By selectively storing and recomputing intermediate activations during the backward pass, we can reduce memory usage and enable the training of larger models or efficient utilization of limited resources. However, it’s essential to carefully weigh the trade-offs associated with additional computational overhead and algorithmic complexity.

As deep learning research progresses, techniques like gradient checkpointing continue to play a vital role in pushing the boundaries of what can be achieved in the field. With ongoing advancements, we can expect further improvements and refinements to enhance the efficiency and effectiveness of deep learning models.

I hope you found this introduction to gradient checkpointing insightful! If you want to delve deeper into this topic, I recommend exploring research papers and resources that discuss gradient checkpointing in more detail.

Gradient Checkpointing