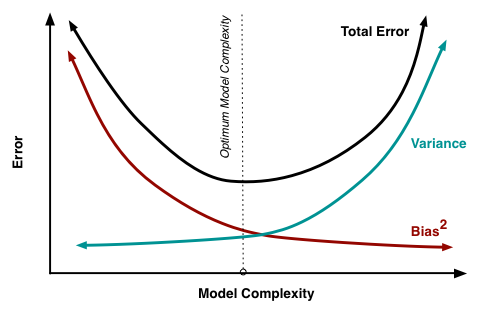
It’s critical to understand prediction mistakes whenever we talk about model prediction (bias and variance). The capacity of a model to minimise bias and variation is subject to a tradeoff. Gaining a good comprehension of these inaccuracies will assist us not just in developing correct models, but also in eliminating the errors of overfitting and underfitting.
Machine learning models are a powerful tool for making predictions based on data. However, as the famous statistician George Box once said, “All models are wrong, but some are useful.” One of the key concepts in understanding how to make a model useful is the bias-variance tradeoff.
What is Bias?
Bias refers to the difference between the predicted values of a model and the true values. Mathematically, we can express this as:
\[Bias = E[\hat{f}(x)] - f(x)\]where \(\hat{f}(x)\) is the predicted value of the model and \(f(x)\) is the true value.
What is Variance?
Variance, on the other hand, refers to the variability of a model’s predictions for a given data point. Mathematically, we can express this as:
\[Variance = E[(\hat{f}(x) - E[\hat{f}(x)])^2]\]The goal in machine learning is to find a model that strikes a balance between bias and variance, as a model with high bias will make strong assumptions about the data and is likely to miss important patterns, while a model with high variance will be sensitive to small fluctuations in the data and is likely to overfit the training data.
As the famous computer scientist David MacKay said, “A model is not a true representation of reality, but an approximation of it.” Therefore, it is important to find a model that generalizes well to new data, that is a model that has a good balance between bias and variance.
One way to achieve this balance is to use a technique called regularization, which is a method of adding a penalty term to the model’s cost function, to reduce the model’s complexity and prevent overfitting. For example, L1 and L2 regularization, which adds the absolute value or square of the model weights to the cost function respectively.
Mathematical illustration :
A simple mathematical example that illustrates the bias-variance tradeoff is linear regression. Linear regression is a model that tries to fit a line to a set of data points. The goal is to find the line that best fits the data, which can be represented mathematically as:
\[y = mx + b\]Where \(y\) is the dependent variable, \(x\) is the independent variable, \(m\) is the slope of the line and \(b\) is the y-intercept.
The bias of this model is the difference between the predicted values of the line and the true values of the data. For example, if we have a set of points \((x_1, y_1), (x_2, y_2), ..., (x_n, y_n)\) and the line that best fits the data is \(y = 2x + 3\), the bias can be calculated as:
\[Bias = \frac{1}{n} \sum_{i=1}^{n} (2x_i + 3 - y_i)^2\]The variance, on the other hand, measures the variability of the model’s predictions for a given data point. For example, if we have a different set of points \((x_1, y_1), (x_2, y_2), ..., (x_n, y_n)\) and the line that best fits the data is \(y = 2.1x + 2.8\), the variance can be calculated as:
\[Variance = \frac{1}{n} \sum_{i=1}^{n} (2.1x_i + 2.8 - E[2x_i + 3])^2\]In this example, a line with a slope of 2 and y-intercept of 3 has a lower bias but a higher variance than a line with a slope of 2.1 and y-intercept of 2.8, as it is a simpler model that makes stronger assumptions about the data, but it may not fit the data as well as the other line. The ideal model is one that strikes a balance between bias and variance and generalize well to new data.
Summary
In summary, the bias-variance tradeoff is a fundamental concept in machine learning and understanding it can help in building more accurate and robust models. The famous statistician John Tukey said, “The combination of some data and an aching desire for an answer does not ensure that a reasonable answer can be extracted from a given body of data.” By understanding the bias-variance tradeoff, we can ensure that our models are reasonable approximations of reality and make more accurate predictions.
Incase of any comments/suggestions please reach out to me on srimouli04@gmail.com
